백준, 4811, 알약

https://www.acmicpc.net/problem/4811

문제

70세 박종수 할아버지는 매일 매일 약 반알을 먹는다. 손녀 선영이는 종수 할아버지에게 약이 N개 담긴 병을 선물로 주었다. 첫째 날에 종수는 병에서 약 하나를 꺼낸다. 그 다음, 그 약을 반으로 쪼개서 한 조각은 먹고, 다른 조각은 다시 병에 넣는다. 다음 날부터 종수는 병에서 약을 하나 꺼낸다. (약은 한 조각 전체 일 수도 있고, 쪼갠 반 조각 일 수도 있다) 반 조각이라면 그 약을 먹고, 아니라면 반을 쪼개서 한 조각을 먹고, 다른 조각은 다시 병에 넣는다. 종수는 손녀에게 한 조각을 꺼낸 날에는 W를, 반 조각을 꺼낸 날에는 H를 보낸다. 손녀는 할아버지에게 받은 문자를 종이에 기록해 놓는다. 총 2N일이 지나면 길이가 2N인 문자열이 만들어지게 된다. 이때, 가능한 서로 다른 문자열의 개수는 총 몇 개일까?

풀이

2N일이 지나면 W, H가 각각 N개로 이루어진 문자열이 생긴다.

그런데 어떤 약 반 조각을 꺼내려면, 그 약을 한 조각으로 꺼낸 날이 그 날보다 먼저 존재해야 한다.
즉 모든 순간에 반드시 (W의 개수 >= H의 개수)가 성립해야 한다.

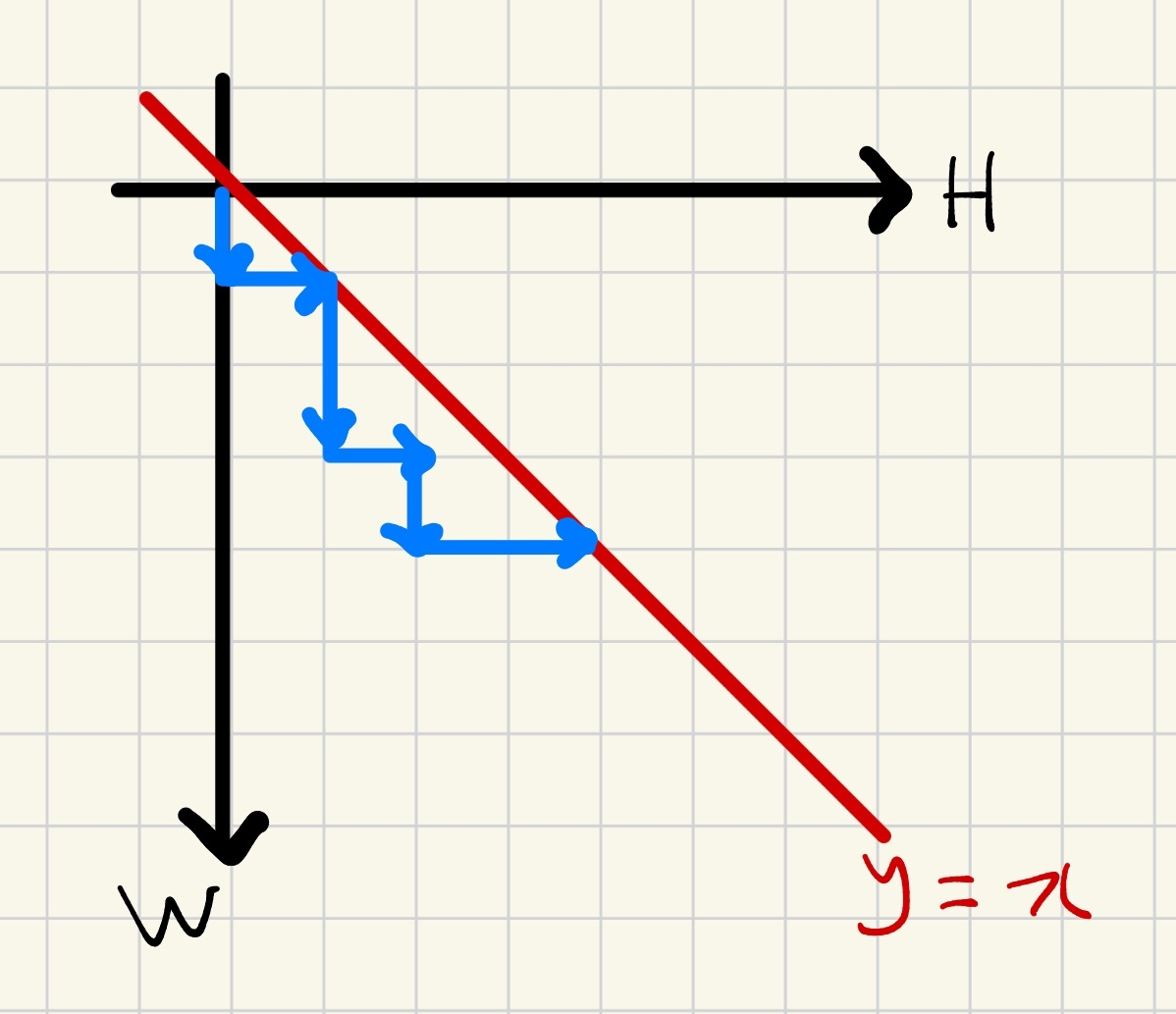
graph

따라서, 문제를 좌표평면의 관점에서 다음과 같이 새로 정의할 수 있다.

W 혹은 H을 1씩 증가시켜 이동해야 한다.
원점에서 시작해 (N, N)까지 이동해야 한다.
y <= x 영역에서 이동해야 한다.

이때 어떤 점 (x, y)까지 이동할 수 있는 경우의 수는, (x-1, y)와 (x, y-1)에서의 경우의 수의 합이다.
이를 코드로 작성하면 다음과 같다.

#include <stdio.h>

int main() {
    
    long long dp[31][31];
    
    for (int i=0; i<31; i++) {
        for (int j=0; j<=i; j++) {
            if (j == 0) dp[i][j] = 1;
            else if (i == j) dp[i][j] = dp[i][j-1];
            else dp[i][j] = dp[i][j-1] + dp[i-1][j];
        }
    }

    while (1) {
        
        int n;
        scanf("%d", &n);
        if (n == 0) break;
       
        printf("%lld\n", dp[n][n]);
    } 
}

백준, 4811, 알약

문제#

풀이#

문제

풀이